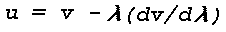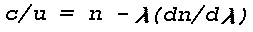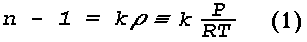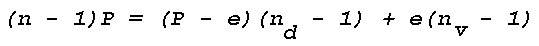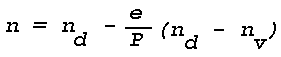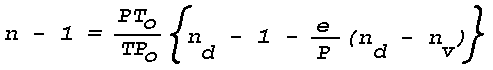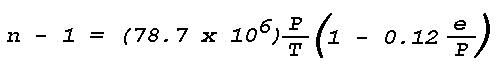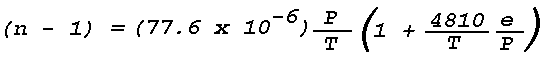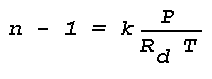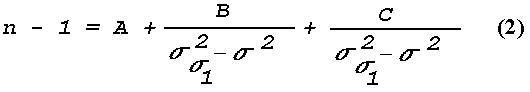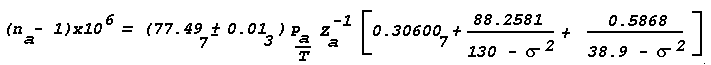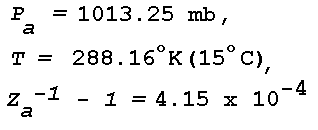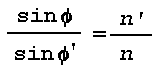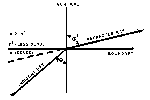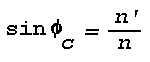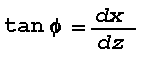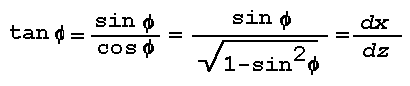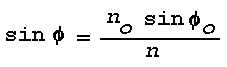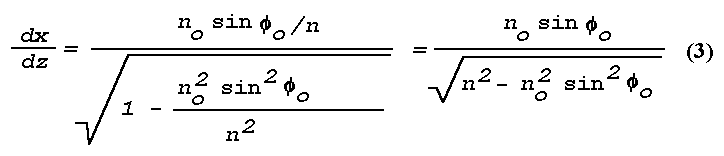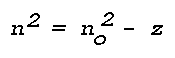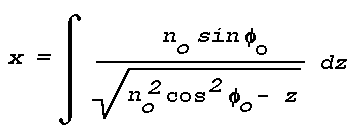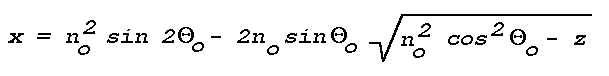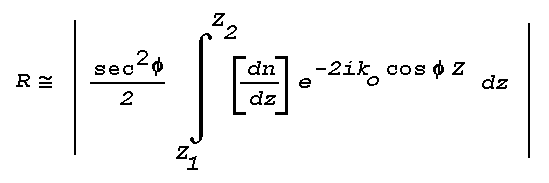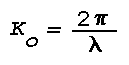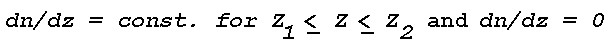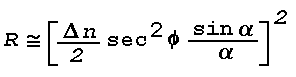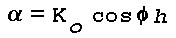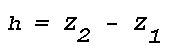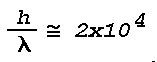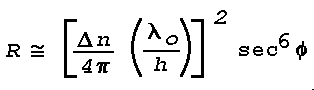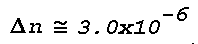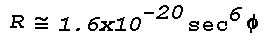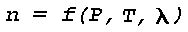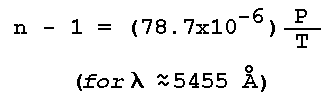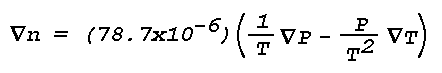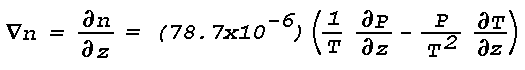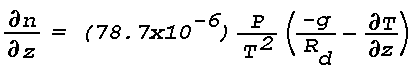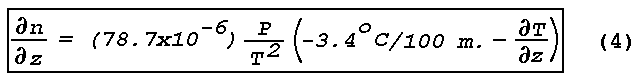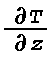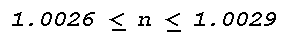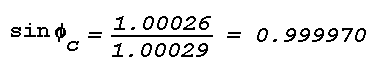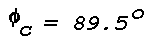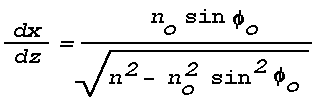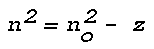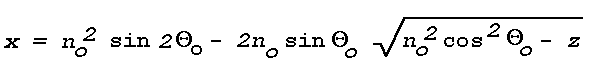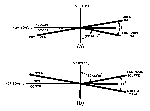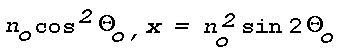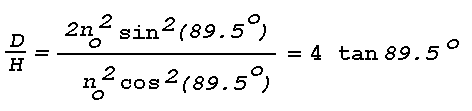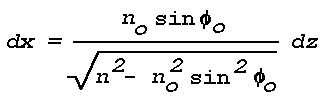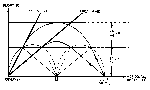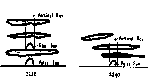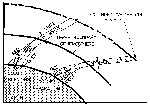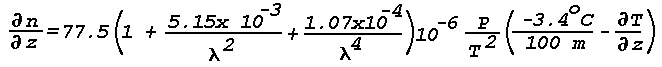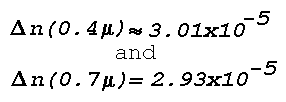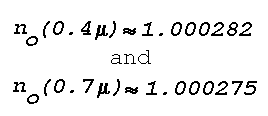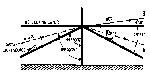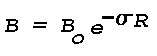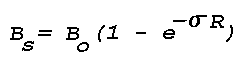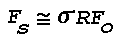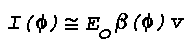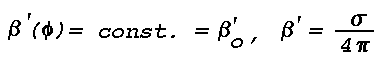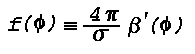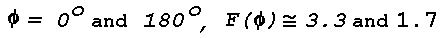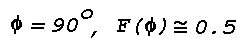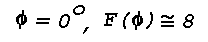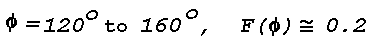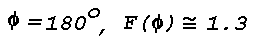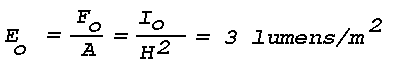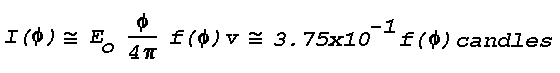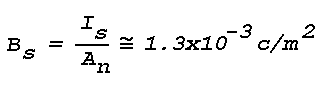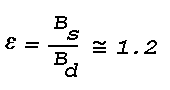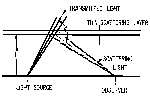
Figure 16: Light Scattering Geometry
Click on Thumbnail to see Full-size image.
[[1049]]
the ground; the total optical depth of the composite atmosphere will
be 0.22. The value of
Sigma appropriate to the haze layer is
2x10
-2 m
-1,
a factor of 10
3 greater than for the "clear" atmosphere
above and below.
To an observer on the ground, the additional extinction of light
caused by the presence of the haze layer, amounting to only 1.6% of
the incident light from a source near the zenith, would not be
perceptible except possibly very close to the horizon. However, light
scattered out of an intense beam by the haze layer could be easily
visible. Assume that a fairly powerful light source is aimed straight
up from the ground; taking as typical values, e.g., for an automobile
sealed beam unit, an intensity, Io, of
3x104 candles (30,000 candlepower) and a beam width of
6°, the light flux Fo incident on the layer at
h = 100 m is 236 lumens, neglecting attenuation in the
air below the layer. The beam solid angle, wo, is
7.85xl0-3 steradians. The incident illuminance,
Eo, on the layer is
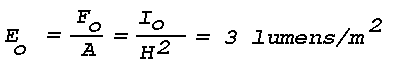
where the illuminated area,
A = woh2,
is 78.5m2. The scattering volume, v, is
78.5m3 since the layer is one meter thick, and the
intensity of the scattered light is
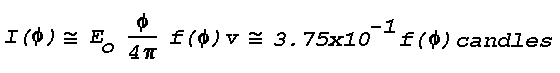
If an observer is located 100 m from the light source, he will
observe the scattered light at a distance of ~140 m and a
scattering angle, Phi, of 135°. The apparent source of the
scattered light will appear to be elliptical, roughly 4° wide and
3° high, and will present an area normal to the observer,
An, of 62.6 m2. The value of
f(Phi) for a strongly scattering medium at
Phi = 135° is about 0.2; therefore the light
Is scattered toward the observer is approximately
7.5x10-2 candles, and the apparent brightness, B,
of the scattering volume will be
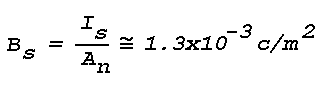
[[1050]]
A fairly dark, moonless night sky has a background brightness,
Bb of about 10
-3 c/m
2;
the scattered image would therefore have a total brightness of
~2.2x10
-3 c/m
2 and a contrast against the
night sky of
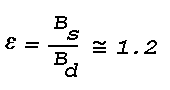
At this background brightness, data given by Middleton (1952) show
that the contrast required for 50% probability of detection for an
object of 3°-4° diameter is about 5.7x10-2; thus
the image hypothesized in this example would have a brightness about
20 times greater than the minimum detectable, and would no doubt be
easily visible as a pale, glowing, elliptical object.
In contrast, the air immediately above and below the haze layer with
Sigma = 2x10-5 m-1
and
f(Phi) ~ 1.1
at
Phi = 135°
would yield a scattered brightness of only about
6.6x10-6 c/m2 per meter thickness. The
contrast against the night sky of the light scattered from the beam
above or below the layer would therefore be on the order of
7x10-3, which is not detectable with a background
brightness of 10-3 c/m2 according to
Middleton (1952).
Increasing the background brightness to
10-2 c/m2, corresponding to a bright,
moonlit night, would decrease the contrast of the scattered image to
1.2x10-1, which is about six times the minimum detectable
contrast at that background brightness and the image would therefore
still constitute a fairly obvious (object). Perception of light
scattered from the rest of the beam under this increased background
brightness, with
Epsilon = 6.6x10-4,
would be out of the question.
The level of background brightness for which the contrast of the
image in this example would be reduced to the point where there is
only a 50% probability of detection by an observer looking in the
right direction is roughly 10-1 c/m2; this
value corresponds to the brightness of a clear sky about 1/2 hour
after sunset.
Thus, scattering of light from sources of small beam width by
localized haze layers in the lower atmosphere may cause the
appearance of diffuse, glowing patches of light, moving with movement
of the light source, that could easily be interpreted as a UFO by an
observer unfamiliar with such phenomena. Data given by Middleton
(1952) show that with common light sources and under average
nighttime sky conditions, the main beam
[[1051]]
of light could easily be imperceptible by scattered light, while at
the same time the light scattered from a haze patch or layer would be
easily visible to an observer; thus the source of the UFO-like image
would not be apparent.
BACK To Section 4
BACK To Top
During the last decade, active interest in optical mirage appears to
have waned. The reasons for the apparent decline are believed to be
two-fold. Firstly, on the basis of simple ray-tracing techniques,
the mirage theories satisfactorily explain the various large-scale
aspects of observations. Thus no disturbing contradictions between
theory and observation have been found. Secondly, although
atmospheric refraction remains of great interest to astronomy,
optical communication, and optical ranging, the phenomenon of the
mirage has so far failed to demonstrate a major use.
At the present time, there is no single theoretical model that
explains all the aspects, both macroscopic and microscopic, of the
mirage phenomenon. The absence of such a model must stand as evidence
that shortcomings remain in current knowledge. These shortcomings are
most eloquently discussed by Sir. C. V. Raman (1959), who suggests
and actually demonstrates that any approach to explain the phenomenon
must be based on wave-optics rather than ray-optics. The theory of
wave-optics, as applied by Sir. C. V. Raman, suggests the presence of
some intriguing aspects of the mirage that arise from the
interference and focussing of wavefronts in selected regions of the
refracting layer. Raman's experimental studies reveal that when a
collimated pencil of light is incident obliquely on a heated plate in
contact with air, the field of observation exhibits a dark region
adjacent to the plate into which the incident radiation does not
penetrate, followed by a layer in which there is an intense
concentration of light and then again by a series of dark and bright
bands of progressively diminishing intensity.
Further theoretical and experimental investigations are warranted in
order to determine to what extent the brightening and brightness
variations that arise from interference and focussing can add unusual
effects to observations of phenomenon associated with abnormal
refraction in the atmosphere.
[[1052]]
BACK To Top
When an unusual optical phenomenon is observed in the atmosphere, its
positive identification as a mirage cannot be made without a
physically meaningful description of what is seen and a complete set
of meteorological and astronomical data. The required "hard" data are
practically never available for the specific place and time of
observation, so that the descriptive account remains the only basis
for identification; in this case, successful identification depends
on a process of education. Thus, the casual observer of an optical
phenomenon can establish the likelihood that his observation is a
mirage only by being aware of the basic characteristics of mirage and
the physical principles that govern its appearance and behavior.
The conditions required for mirage formation and the principal
characteristics of mirage images, as described in this report, are
summarized below. The summary presents a set of standards by which to
interpret the nature of an optical observation in terms of a specific
natural atmospheric phenomenon.
A. Meteorological Conditions
Optical mirages arise from abnormal temperature gradients in the
atmosphere. A temperature decrease with height (temperature lapse)
exceeding 3.4°C per 100 m or a temperature increase with height
(temperature inversion) is most commonly responsible for a mirage
sighting.
Large temperature lapses are found in the first 10 meters above the
ground during daytime. They occur when ground surfaces are heated by
solar radiation, while during nighttime they can occur when cool air
flows over a relatively warm surface such as a lake. When the
temperature decreases with height more than 3.4° per 100 m
over a
horizontal distance of 1 kilometer or more, an observer located
within the area of temperature lapse can sight an inferior mirage
near the ground (e.g., road mirage, "water" on the desert)
Layers of temperature inversion ranging in thickness from a few
meters to several hundred meters may be located on the ground or at
various levels above it. In areas where they are horizontally
extensive, an observer can sight a superior mirage that usually
appears far away (beyond 1 kilometer) and "low in the sky." The
strength of the inversion determines the degree of image-elevation;
the stronger the inversion, the higher the image appears above the
horizon. Layers of maximum temperature inversion (30°C) are
usually found adjacent to the ground.
[[1053]]
Calm, clear-weather conditions (no precipitation or high winds) and
good horizontal visibility are favorable for mirage formation. Warm
days or warm nights during the summer are most likely to produce the
required temperature gradients.
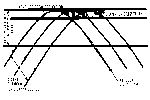
B. Geometry of Illumination and Viewing
The geometry of illumination and viewing in the case of optical
mirage is determined by the spatial variations of refraction index
that occur in the cloud-free atmosphere, and by Snell's law of
refraction, which relates these variations to changes in the
direction of propagating wavefronts. The spatial variations in
refractive index are associated with layers of temperature inversion
or temperature lapse. Variations of 3x10-5, corresponding
to temperature changes of 30°C, are considered near maximum. As
a
consequence of Snell's law and the small changes in the atmospheric
refractive index, an optical mirage develops only when a temperature
inversion layer or a layer of large temperature lapse is illuminated
at grazing incidence. The requirement of grazing incidence implies
that the source of illumination must be either far away, i.e., near
the horizon, or very close to or within the layer of temperature
gradient. Therefore, both terrestrial and extraterrestrial sources
can be involved. Because of the distance factor, the actual source of
illumination may not be visible. Its location, however, must always
be in the direction in which the mirage image is observed, i.e.,
observer, image and "mirrored" source are located in the same
vertical plane.
Another consequence of Snell's law and the small spatial changes in
refractive index is that noticeable refractive effects are not likely
beyond an angular distance of approximately 14 degrees above the
horizon and that a superior mirage image is not likely beyond an
angular distance of 1 to 2 degrees above the horizon. Hence, mirages
appear "low in the sky" and near the horizontal plane of view. An
optical image seen near the zenith is not attributable to mirage.
Because of the restricted geometry between observer, mirage image,
and source of illumination, the observed image can often be made to
disappear abruptly by moving to higher or lower ground. Furthermore,
when mirage
[[1054]]
observations are made from a continuously moving position, the image
can move also, or can move for a while and then abruptly disappear.
C. Shape and Color
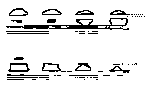
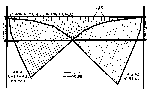
A mirage can involve more than one image of a single object.
Observations of up to four separate images, some inverted and some
upright, are encountered in the literature. When multiple images
occur they all lie in a single vertical plane or very close to it.
The apparent shape of a mirage can vary from clearly outlined images
of an identifiable object such as a distant ship, landscape, or the
sun or moon, to distorted images that defy any description in terms
of known objects (e.g., Fata Morgana). Apparent stretching either in
the vertical or in the horizontal plane is common.
During daytime, a mirage can appear silvery white ("water" on the
ground), or dark when projected against a bright sky background, or
it can reflect the general color of the land or seascape. Distinctly
colored images ranging from red and yellow to green and blue are
observed when unusual conditions of mirage occur near sunrise or
sunset (e.g., Red and Green Flash) or, at night, during rising or
setting of the moon or of a planet such as Venus.
In the presence of atmospheric turbulance and convection, the effects
of scintillation become superimposed on the large-scale mirage image.
When scintillation occurs, extended mirage images appear in constant
motion by changing their shape and brightness. When the image is
small and bright, as may be the case at night, large fluctuations in
brightness and under unusual conditions in color can give an illusion
of blinking, flashing, side to side oscillation, or motion toward and
away from the observer. The effects associated with scintillation can
dominate the visual appearance of any bright point-object in the area
between the horizon and approximately 14 degrees above the horizon.
D. Present Uncertainties
The theory of ray optics adequately explains such observed
large-scale aspects of the mirage as the number of images, image
inversion, and apparent vertical stretching and shrinking. However,
if the interference and focussing of wavefronts within the refracting
layer are as fundamental
[[1055]]
in mirage formation as purported by Sir C.V. Raman, the ray-tracing
technique may have to be replaced by the theory of wave-optics.
Sir C. V. Raman's application of wave-optics to mirage suggests that
under special conditions of illumination, the upper boundary of an
atmospheric temperature inversion could exhibit a large
concentration of radiant energy due to focussing of wavefronts. Also,
interference of wavefronts could produce alternating layers of high
and low brightness. Under what conditions and to what extent these
brightness effects can be observed in the atmosphere is not known.
Relevant observations have not been encountered in the literature,
although some unusual observations of the green flash made under
mirage conditions (O'Connel, 1958) could possibly have been caused by
the enhancement of brightness in an inversion. The visual effects
from focussing and interference of wavefronts must be considered as
the least explored aspect of mirage.
[[1056]]
BACK To Top
Benson, Carl S., "Ice Fog: Low Temperature Air Pollution,"
Geophysical Inst., Univ. of Alaska (November 1965).
Brocks, K., Vertikaler Temperaturgradient und terrestrische
Refraction, inshesondere ira Nochgebrge. (Verlag von Dietrich
Reimer Andrews t~ Steiner, Berlin 1939).
Dietze, Gerhard, Einfuhrung in die Optik der Atmosphare
(Akademische Verlagsgesellschaft, Geest & Portig K. - G., Leipsig
1957).
Eldridge, Ralph G., "Climatic Visibilities of the United States,"
J. Appl. Meteorol., Vol. 5, No. 3 (June 1966).
Epstein, Paul S., "Geometrical Optics in Absorbing Media," Proc.
Nat. Acad. Sci.,Vol. 16, 37-45 (1930).
Epstein, Paul S., "Reflections of Waves in an Inhomogeneous Absorbing
Medium," Proc. Nat. Acad. Sci., Vol. 16, No. 10,628-637 (October
1930).
Goos, F. and H. Haenchen, "A new and fundamental experiment on total
reflection," Ann. Physik ,Vol. 6, No. 1, pp. 333-346 (1947).
Handbook of Geophysics and Space Environments, Chapter 13, Air
Force Cambridge Research Laboratories, Office of Aerospace Research,
USAF (1965).
Hosler, Charles R., "Low-level inversion frequency in the contiguous
United States," Monthly Weather Rev., Vol. 89, No. 9 (September
1961).
Humphreys, C. E., Physics of the Air (McGraw-Hill Book Company,
Inc., New York 1940).
Jenkins, F. A., and H. E. White, Fundamentals of Optics, 3rd
Ed.
(McGraw-Hill Book Company, Inc., New York 1957).
Johnson, John C., Physical Meteorology (Published jointly by
the
Technology Press of M.I.T. and John Wiley & Sons, Inc., New York
1954).
Lane, J.A., "Some investigations of the structure of elevated layers
in the troposphere," J. of Atmos. and Terres. Phys., Vol. 27,
pp.
969-978
Middleton, W. E. Knowles. Vision Through the Atmosphere,
University of Toronto Press, 1952.
[[1057]]
Minnaert, M.,
The Nature of Light and Colour in the Open Air
(Dover Publications, Inc., 1954).
Neuberger, Hans, General Meteorological Optics, in Compendium
of Meteorology (American Meteorological Society, Boston, Mass.,
(1951).
O'Connel, D. J. K., The Green Flash and Other Low Sun Phenomena,
Vatican Observatory (North Holland Publishing Company, Amsterdam;
Interscience Publishers, Inc., New York, 1958).
Owens, James C., "Optical Refractive Index of Air: Dependence on
Pressure, Temperature and Composition," Applied Optics, Vol.
6,
No.1 (January 1967).
Pernter, J. M. and Felix M. Exner, Meteorologische Optik, (Wien
und Leipzig, Wilhelm Braumuller, K. U. K. Hofund
Universitats-Buchhandler, 1910).
Ramdas, L. A., "Micro-Climatological Investigations in India,"
Archiv. fur Meteorologie, Geophysik und Bioklimatologie, Ser.
B,
Vol. 3 (1951).
Sears, F. W., Optics (Addison-Wesley Press, Inc., Cambridge,
Mass., 1949).
Tolansky, S., Optical Illusions (Pergamon Press, New York 1964).
Visher, S. S., Climatic Atlas of the United States (Harvard Univ.
Press, Cambridge, Mass. ,1954).
Wallot, S., "Der senkrechte Durchgang elektromagnetischer Wellen
durch eine Schicht raumlich veranderlicher Dielektrisitats
konstante," Ann. Physik, Vol. 60, pp. 734-762 (1919).
Wood, Robert W., Physical Optics, 3rd ed., (The MacMillan
Company, New York,1934).
[[1058]]
BACK To TOP